Modelling Cellular Kinematics in Self-Similar Plant Growth
Biophysics Internship - 2025
Cover image credit from Figure 3 of (Prusinkiewicz & Runions, 2012).
Some plant structures exhibit self-similar growth, that is, they maintain stable geometries as their cells grow, divide, and flow within them. This offers an analytically tractable system for exploring their growth kinematics and the coupling between genetic regulation and morphoelasticity in plant development. After first trying to examine the PDEs governing the system analytically we then used a custom numerical solver for morphodynamics, namely Organism, to create models to emulate these forms, capturing cellular growth and proliferation while preserving overall geometry.
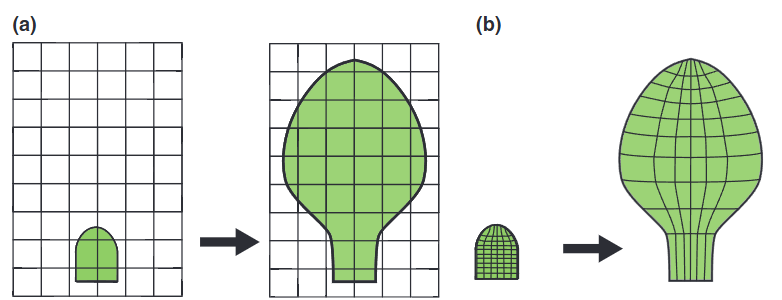
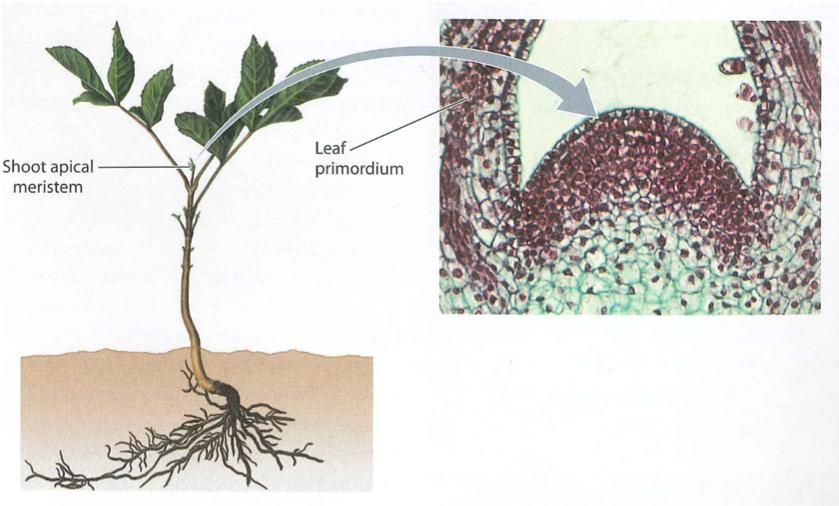
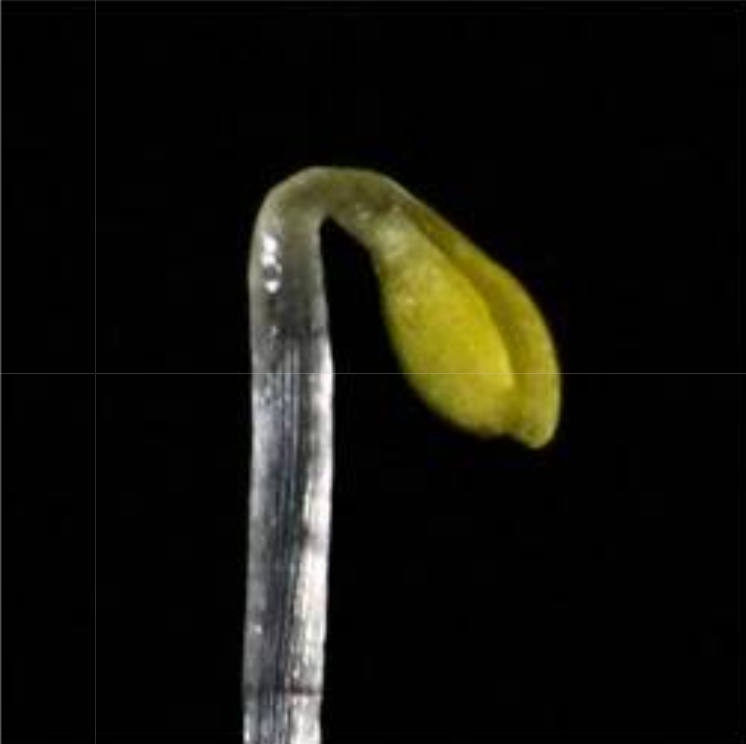
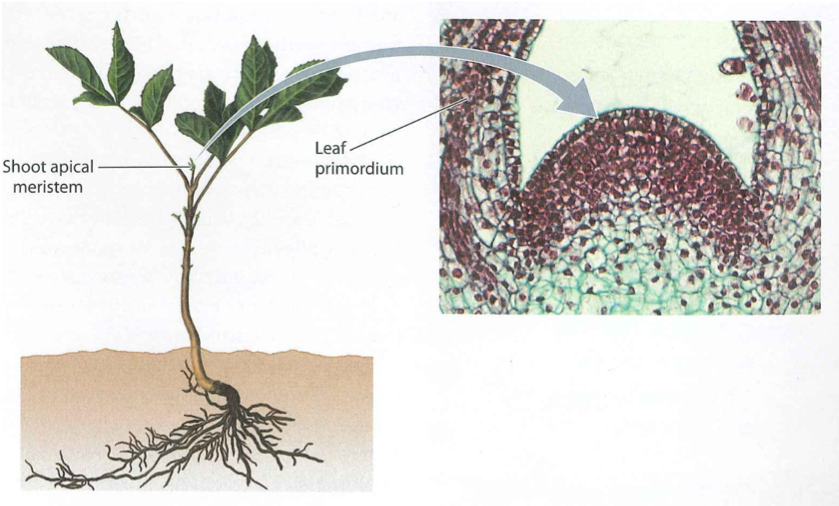
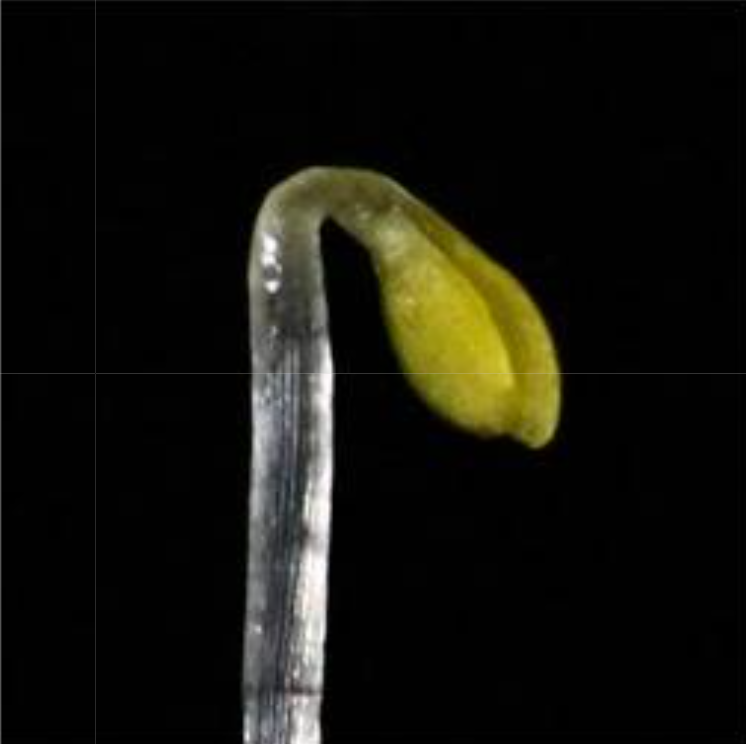
Specifically, we looked at emulating the Shoot Apical Meristem (SAM) and the apical hook as shown in Figure 1. We did this by performing a map between Lagrangian, curvilinear and Eulerian coordinate systems. A parabolic map was used to model the SAM and is given by \(\begin{equation} \begin{split} s &\mapsto x = sr \\ r &\mapsto y = \frac{1}{2}(r^2 - s^2) \,, \label{ODE} \end{split} \end{equation}\) where $(s,r)$ span the curvilinear space and $(x,y)$ span the Eulerian space. The apical hook required the more complicated transformation \(\begin{equation} \begin{split} \theta(s) &= \int\limits_0^s d\tilde{s} \, \kappa(\tilde{s}) \\ x(s,r) &= \int\limits_0^s d\tilde{s} \,\sin(\theta(\tilde{s})) + r\cos(\theta(s)) \\ y(s,r) &= \int\limits_0^s d\tilde{s} \, \cos(\theta(\tilde{s})) - r\sin(\theta(s)) \end{split} \end{equation}\) where $\kappa=\kappa(\tilde{s})$ is the curvature distribution–we used a gamma distribution.
The resultant models are shown in Figure 2. The cells flow within a fixed envelope while growing and dividing. By keeping the curvilinear space the same (up to length scales) and solely varying the map to the Eulerian space, completely different plant structures can be replicated. Gene regulatory networks can then be placed on these structures and coupled to growth mechanics in the orthogonal, $r$, direction.
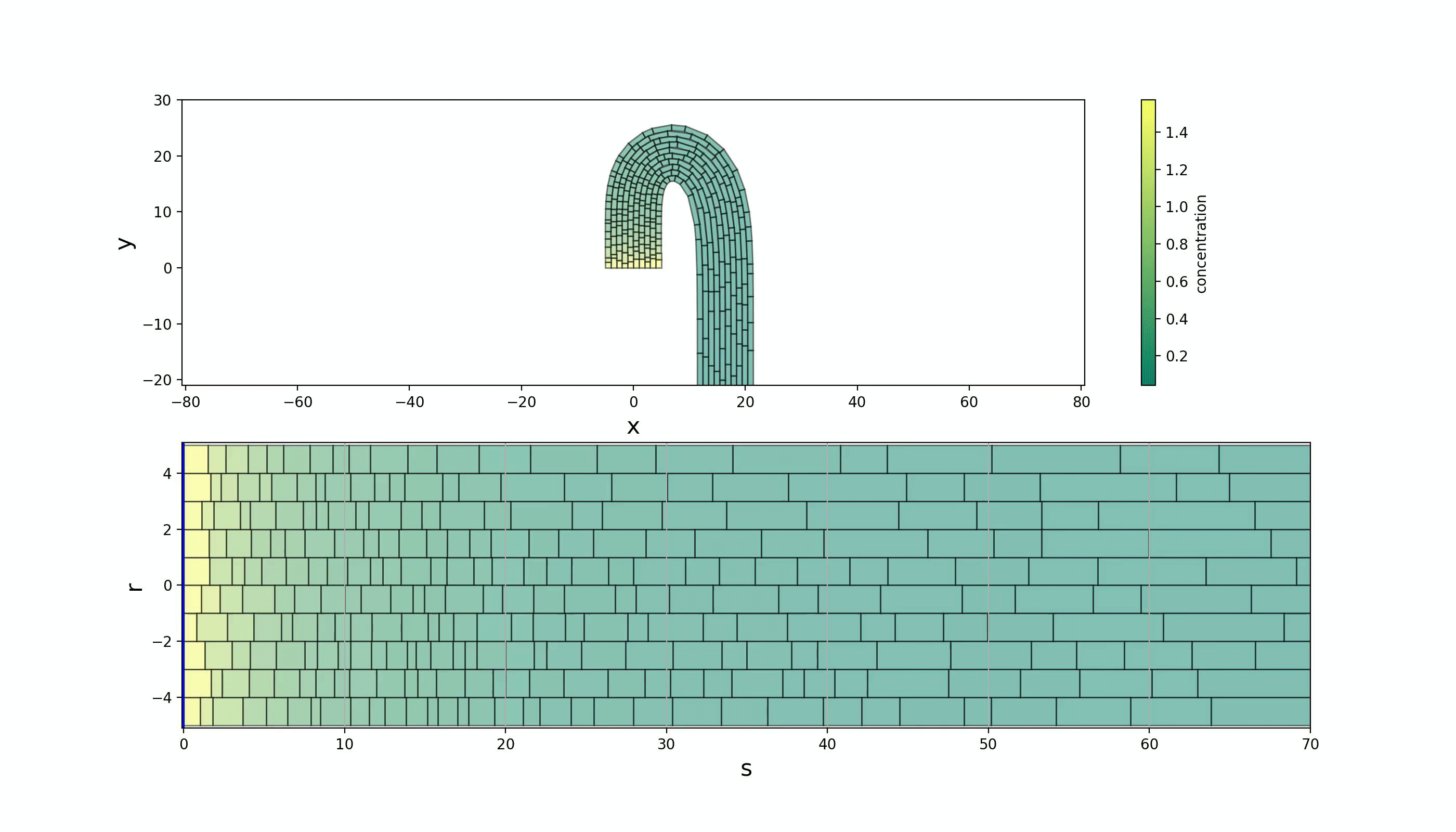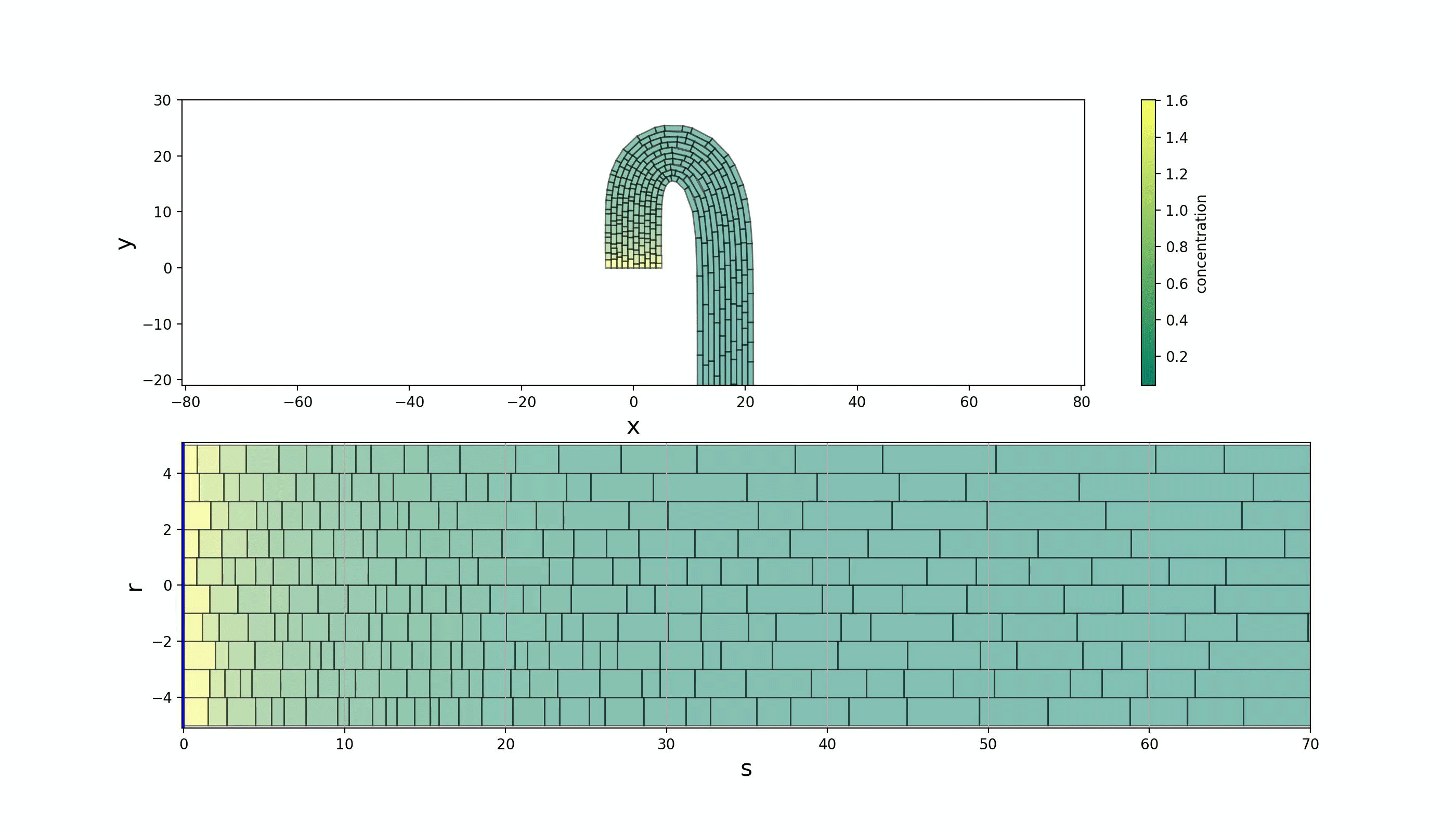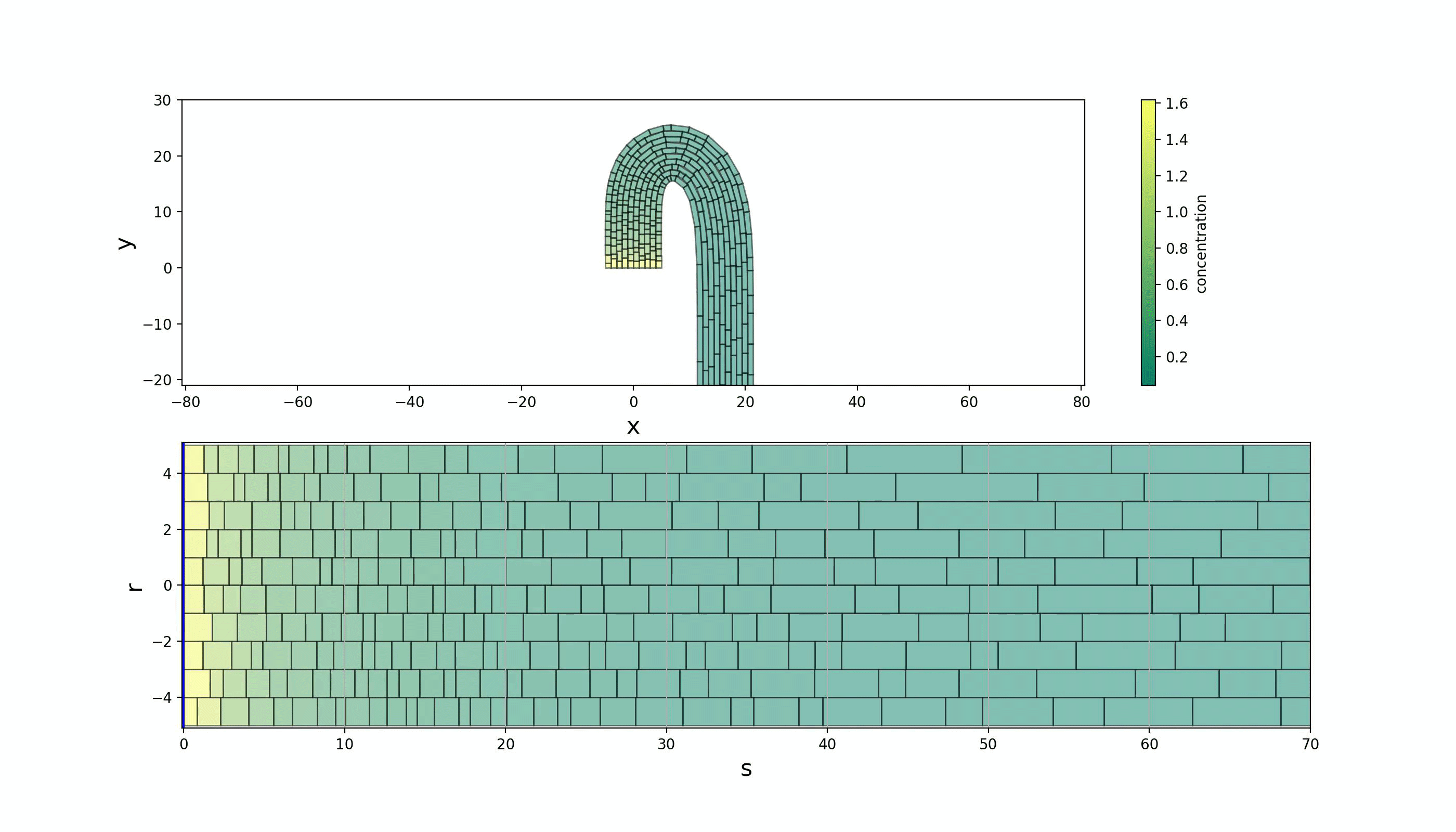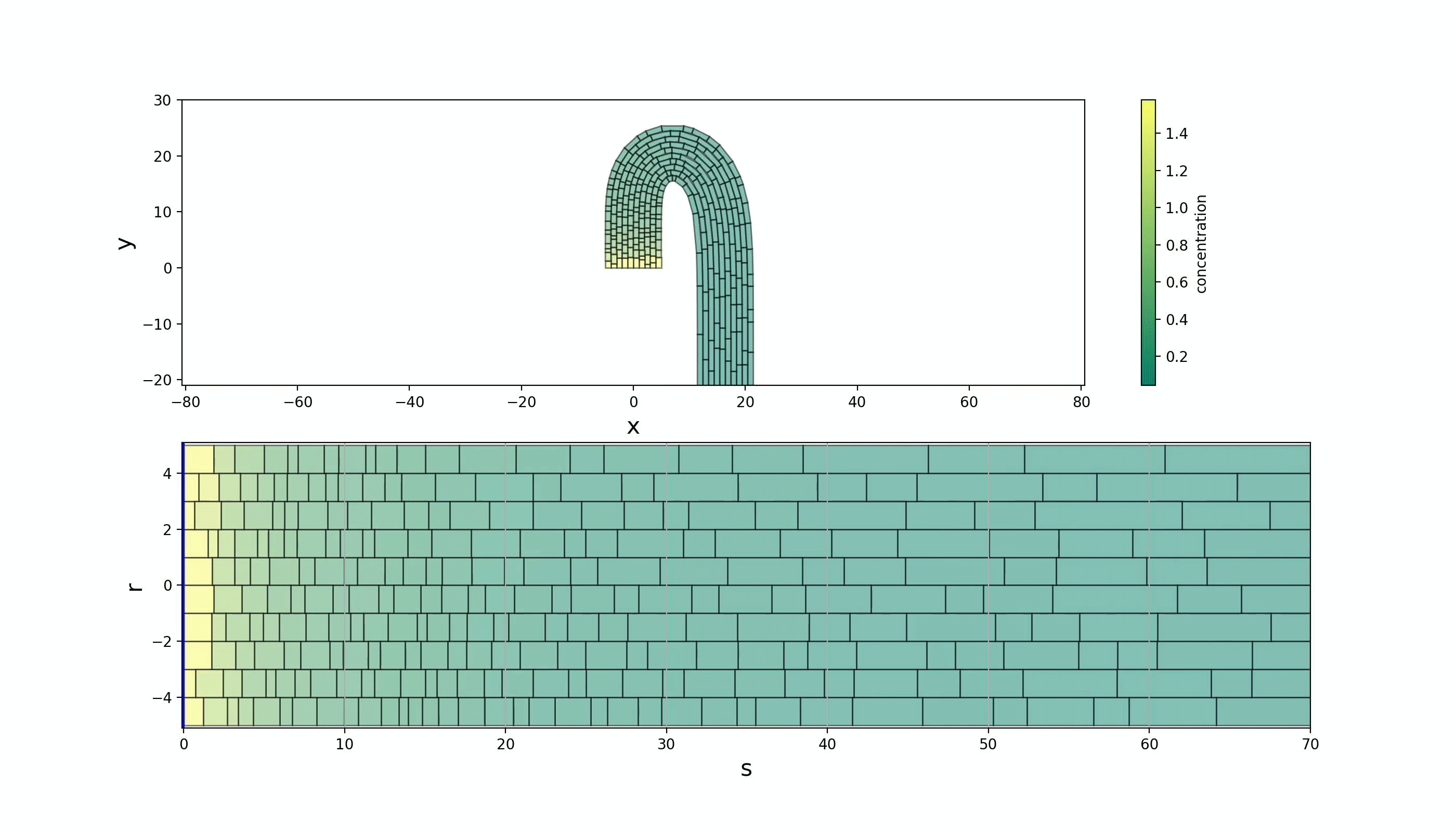
References
2025
-
 VCU BIOL 152: Introduction to Biological Sciences II2025Richmond (VA): Virginia Commonwealth University
VCU BIOL 152: Introduction to Biological Sciences II2025Richmond (VA): Virginia Commonwealth University
2020
-
 Salicylic acid suppresses apical hook formation via NPR1-mediated repression of EIN3 and EIL1 in ArabidopsisThe Plant Cell, 2020
Salicylic acid suppresses apical hook formation via NPR1-mediated repression of EIN3 and EIL1 in ArabidopsisThe Plant Cell, 2020